Glossaire
Comparaison statistique de données
Afin de déterminer si une donnée est statistiquement différente d’une autre, on peut utiliser les intervalles de confiance (I.C.). En général, si les intervalles de confiance se chevauchent, on considère que les valeurs ne sont pas statistiquement différentes. À l’inverse, si les intervalles de confiance ne se chevauchent pas, les valeurs sont considérées statistiquement différentes.
Cependant, cette règle peut avoir des exceptions. Il est possible, bien que rare, que des intervalles de confiance se chevauchent tout en révélant une différence significative selon la valeur p obtenue par un test statistique (comme le test Z). À l’opposé, des intervalles non chevauchants peuvent parfois ne pas correspondre à une différence statistiquement significative selon les critères du test utilisé.
Un exemple d’écart non statistiquement significatif selon les I.C.:
Prenons l’exemple réel de la prévalence du TDA/H en Gaspésie‒Îles-de-la-Madeleine en 2021-2022. Elle est estimée à 6,3 % (I.C. : 5,9 – 6,8), comparée avec la valeur du Saguenay-Lac-Saint-Jean à 5,7 % (I.C. : 5,5 – 6,0). Comme les intervalles de confiance des deux régions se chevauchent, l’écart de 0,6 % observé entre ces deux régions n'est pas considéré statistiquement significatif, i.e. on ne peut pas conclure que la prévalence du TDA/H est plus élevée en Gaspésie‒Îles-de-la-Madeleine qu’au Saguenay-Lac-Saint-Jean.
Un exemple d’écart statistiquement significatif selon les I.C :
Prenons toujours l’exemple de la Gaspésie‒Îles-de-la-Madeleine pour la prévalence du TDA/H dont la valeur est de 6,3 % (I.C. : 5,9 – 6,8), comparée avec la valeur de Chaudière-Appalaches à 4,7 % (I.C. : 4,6 – 4,9). Comme les intervalles de confiance des deux régions ne se chevauchent pas, l’écart observé de 1,6 % entre ces deux régions est considéré statistiquement significatif, i.e. on peut conclure que la prévalence du TDA/H est plus élevée en Gaspésie‒Îles-de-la-Madeleine qu’en Chaudière-Appalaches.
Plus de détails sont disponibles sur les intervalles de confiance et les seuils alpha dans la section Intervalles de confiance.
Espérance de vie
L’espérance de vie à la naissance correspond au nombre moyen d’années qu’une personne peut espérer vivre si toute sa vie se déroulait selon les conditions de mortalité observées au cours d’une année donnée.
C’est un indicateur couramment utilisé pour résumer l’état de santé d’une population à un moment précis. Il est également comparable à la fois dans le temps et avec d’autres territoires où les décès sont bien enregistrés. Cependant, comme le calcul d’espérance de vie s’appuie sur des taux de mortalité fixes dans le temps, la valeur d’espérance de vie d’une année donnée ne doit pas être utilisée comme une prédiction du nombre moyen d’années que vivront les personnes nées lors de cette même année.
Par exemple, l’espérance de vie s’élevait à 82,5 ans en 2023 au Québec. Il est raisonnable de s’attendre à ce que la durée de vie moyenne des personnes nées en 2023 soit supérieure à cette valeur, notamment grâce aux futurs progrès futurs médicaux.
Incidence
L’incidence correspond au nombre de nouveaux cas d’une maladie au cours d’une période donnée. À ne pas confondre avec la prévalence, qui représente le nombre total de personnes atteintes par la maladie à un moment donné, qu’il s’agisse de cas récents ou anciens.
Intervalles de confiance (I.C.)
L’intervalle de confiance est une mesure statistique de la précision d’une estimation. Une incertitude plus ou moins grande est toujours rattachée aux nombres, taux ou proportions présentés. Un intervalle de confiance représente l’étendue de valeurs possibles pour l’indicateur en question. Il est exprimé sous la forme de deux chiffres qui indiquent les bornes inférieure et supérieure de cette étendue. Plus l’étendue de valeurs est étroite, plus la donnée est précise; plus elle est large, plus elle est imprécise. L’étendue de l'I.C. renseigne également sur la taille de l'échantillon. Plus l'échantillon est grand, plus la variabilité d'échantillonnage est faible, et plus l’I.C. est étroit.
Les intervalles de confiance sont également utilisés pour déterminer si l’écart entre deux estimations est statistiquement significatif. Consultez la section Comparaison statistique de données pour en connaître davantage sur l’utilisation des I.C. pour comparer des données.
Un I.C. dont le niveau de confiance s’élève à 99 % (soit un seuil alpha de 0,01) correspond à une plage de valeurs estimée dans laquelle la valeur réelle devrait se situer 99 fois sur 100.
Un I.C. dont le niveau de confiance s’élève à 95 %, soit un seuil alpha de 0,05, correspond à une plage de valeurs estimée dans laquelle la valeur réelle devrait se situer 95 fois sur 100, ou 19 fois sur 20.
Voici un exemple :
En 2021-2022, la prévalence du TDA/H en Gaspésie‒Îles-de-la-Madeleine est estimée à 6,3 % avec un intervalle de confiance entre 5,9 % et 6,8 % à un niveau de confiance de 99 %. En d’autres termes, si un rééchantillonnage avait lieu, la prévalence du TDA/H en GaspésieÎles-de-la-Madeleine serait située entre 5,9 % et 6,8 % et ce, 99 fois sur 100.
Voici un tableau récapitulatif du seuil alpha utilisé pour les indicateurs selon la source de données :
| Source de données | Ensemble du Québec1 | Régions sociosanitaires ou autre croisement (ex : âge) |
| Registre des événements démographiques (Fichier des décès et des naissances, Ministère de la Santé et des Services sociaux (MSSS)). | I.C. à 99 % (seuil 0,01) | I.C. à 95 % (seuil 0,05) |
SISMACQ (Système intégré de surveillance des maladies chroniques du Québec) | I.C. à 99 % (seuil 0,01) | I.C. à 99 % (seuil 0,01) |
| Recensement | Non applicable | Non applicable |
| Enquête québécoise sur la santé de la population (EQSP) | I.C. à 99 % (seuil 0,01) Incluant croisements selon l’âge et autres variables de croisements | I.C. à 95 % (seuil 0,05) |
| Enquête québécoise sur la santé des jeunes du secondaire (EQSJS) | I.C. à 95 % ou 99 % dépendamment de l’indicateur | I.C. à 95 % (seuil 0,05) |
1 Pour les indicateurs du Registre d’événements démographiques, le seuil de l’IC pour l’ensemble du Québec est de 95 % dans les graphiques 3.1b (lorsque comparé aux régions sociosanitaires). Il est de 99% pour le graphique 1.1. d’évolution au Québec.
Lorsque des taux ou des proportions sont comparés, il arrive souvent que la structure d’âge des populations à partir desquelles ils sont calculés influence le résultat. Par exemple, le taux de mortalité sera nécessairement plus élevé dans une population âgée qu’une population jeune. Pour que les taux ou proportions soient comparés sur un pied d’égalité, il est habituel d’utiliser une population de référence pour procéder à l’ajustement des taux ou proportions, aussi appelé standardisation ou normalisation.
Cette méthode consiste à ajuster mathématiquement une ou plusieurs populations pour leur donner la même structure par âge qu’une population de référence, qui peut être fictive ou réelle. Cet ajustement permet d'obtenir des taux comparables.
Avant de procéder à l’ajustement d’un taux ou d’une proportion, il faut ainsi choisir la population de référence, aussi appelée population type. Pour assurer une homogénéité et une bonne comparabilité entre les résultats publiés par différents groupes, il est préférable d’utiliser des populations de référence dont les structures d’âge ont été publiées et sont largement répandues (Bouyer et autres, 1993).
Voici les populations de référence utilisées pour les taux ajustés des indicateurs:
- Pour les données du Québec au fil du temps :
- la population sexes réunis du Québec de 2016 (RED; Registre québécois du cancer);
- de 2011 (SISMACQ);
- la population de l’EQSP 2020-2021 (EQSP)
- Pour les données des provinces canadiennes :
- la population sexes réunis du Canada de 2021.
- Pour les données des états américains :
- la population sexes réunis des États-Unis de 2000.
Pour les données des pays de l’Organisation de coopération et de développement économiques (OCDE) :
- la population sexes réunis de l’OCDE de 2015.
Puisque les taux et proportions du Québec ont été calculés à l’aide de plusieurs différentes populations de référence, des différences dans les estimations sont attendues en fonction des comparaisons canadiennes, américaines ou internationales.
Référence : Bouyer, J. et autres. (1993). Épidémiologie : Principes et méthodes quantitatives, Paris, France : INSERM.
La prévalence est définie comme le nombre de cas d’une maladie ou d’une condition au cours d’une période donnée dans une population, exprimée en proportion. Elle correspond à une « photographie » d’une maladie dans une population donnée à un moment précis, en incluant à la fois les cas récents et les cas plus anciens encore présents. Elle peut être brute ou ajustée.
Consultez la section Valeurs brutes ou ajustées : comment faire le bon choix ? pour des définitions et un guide pour aider à choisir entre les valeurs brutes et ajustées selon le contexte.
Prévalence à vie et prévalence annuelle
La prévalence à vie, aussi appelée prévalence cumulative, d’une année donnée correspond à tous les individus identifiés par la définition de cas dans l’année ainsi que tous ceux identifiés précédemment.
- Indicateurs se basant sur une prévalence à vie : TSA, prévalence du diabète, de l’hypertension artérielle, des cardiopathies ischémiques, d’asthme, de MPOC, d’Alzheimer.
La prévalence annuelle requiert la requalification annuelle pour qu’un individu soit identifié comme un cas pour une année donnée.
- Indicateurs se basant sur la prévalence annuelle : TDAH, troubles anxio-dépressifs.
Une proportion est un est un rapport entre deux quantités du même groupe, qui permet de comparer une quantité à l’ensemble du groupe. Par exemple, une partie de la population est atteinte de diabète, qui peut être représenté par une proportion. Elle sera ainsi calculée en rapportant le nombre de personnes atteintes de diabète à l’ensemble de de la population : en 2022-2023 parmi la population de 1 an et plus, on compte 713 625 personnes atteintes de diabète parmi une population de 8 592 770. Cela équivaut à une proportion de 8,3 % de la population de 1 an et plus qui est atteinte de diabète.
Une proportion peut être brute ou ajustée. Consultez la section Valeurs brutes ou ajustées : comment faire le bon choix ? pour des définitions et un guide pour aider à choisir entre les valeurs brutes et ajustées selon le contexte.
Le taux est une des mesures de fréquence utilisée pour décrire la mortalité ou la morbidité (présence de maladie) ou dans la population. Il est décrit comme le rapport entre le nombre de nouveaux évènements ou de nouveaux cas, survenus au cours d’une période et la population à risque de développer l’évènement au cours de cette période (Simpson, Beaucage et Bonnier Viger, 2008)
Un taux peut être utilisé lorsque l’on veut comparer des indicateurs ayant des tailles de populations différentes. Par exemple, le nombre de cas dans la région sociosanitaire de Montréal sera sans doute plus élevé que dans la région sociosanitaire du Bas-Saint-Laurent compte tenu de la taille de leurs populations respectives. Pour mieux comparer la situation des deux régions, il est utile de présenter le nombre de cas divisé par leur population respective.
Il existe des taux bruts et des taux ajustés (aussi appelés normalisés ou standardisés). Consultez la section Valeurs brutes ou ajustées : comment faire le bon choix ? pour des définitions et un guide pour aider à choisir entre les valeurs brutes et ajustées selon le contexte.
Le ratio est une mesure de comparaison qui permet d’interpréter l’ampleur des différences entre deux groupes distincts. Le ratio est obtenu en divisant la mesure de santé (taux ou proportion) de l’indicateur dans le groupe A (mesure A) par rapport à celle obtenue dans un groupe de référence (mesure B). Le groupe de référence peut être une population non atteinte de la maladie liée à l’indicateur de santé ou une population atteinte de la maladie, mais appartenant à un autre territoire géographique.
Le ratio est la plupart du temps calculé avec des mesures de santé standardisées selon une structure d’âge, de sexe et d’une référence populationnelle afin que le ratio ne soit pas affecté par les changements de structure de la population.
Le calcul d’un ratio entre deux mesures de santé pour une période donnée est une simple division :
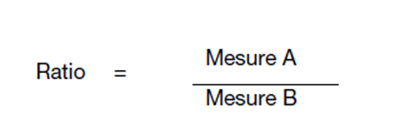
- Un ratio égal à 1 indique qu’il n’y a aucune différence entre les deux groupes.
- Plus le ratio se rapproche de 1, plus la différence entre les groupes est faible.
- Un ratio de 0,5 signifie que la fréquence observée dans le groupe A est deux fois moins élevée que dans le groupe B.
- En revanche, un ratio de 2 indique que la fréquence dans le groupe A est deux fois plus élevée que dans le groupe B.
Cette question revient fréquemment, même chez les utilisateurs expérimentés. Chaque option présente ses avantages et ses limites, et le choix le plus pertinent dépend du contexte spécifique de l’analyse. Il est donc essentiel de bien comprendre les implications de chaque option.
Dans plusieurs graphiques de l’Indicateur de santé publique, l’option de présenter les données selon des valeurs brutes ou ajustées est disponible dans un menu déroulant. Ce choix peut s’appliquer à des taux, des proportions, des prévalences ou des incidences. Voici un rappel des éléments à retenir pour chacune des deux options :
- Les valeurs brutes sont utilisées pour illustrer le fardeau réel du phénomène dans la population. Les valeurs brutes ne sont pas comparables dans le temps ou entre différents territoires lorsque la répartition par âge des populations comparées n’est pas similaire. Par exemple, le taux brut de mortalité sera nécessairement plus élevé dans une population âgée qu’une population jeune.
- Les valeurs ajustées sont utilisées pour comparer un indicateur donné dans le temps ou entre différents territoires. L’ajustement consiste à modifier mathématiquement une ou plusieurs populations afin de leur attribuer la même répartition par âge qu’une population de référence, qui peut être fictive ou réelle. Cette méthode est particulièrement indiquée pour des indicateurs qui varient selon l’âge ou qui sont influencés par le vieillissement de la population. L’ajustement permet d'obtenir des taux comparables entre différents groupes ou périodes. Il est toutefois important de souligner que les valeurs ajustées sont artificielles et n’ont de signification que dans un contexte comparatif, que ce soit dans le temps ou entre territoires.
Voici quelques mises en situation :
- Je veux connaître la proportion de la population atteinte de diabète en 2023.
La proportion brute est de mise dans ce cas-ci, puisqu’elle permet de refléter le fardeau réel de cette maladie au Québec en 2023 et que la valeur n’est pas destinée à être comparée dans le temps.
- J’aimerais étudier l’évolution de la mortalité par cancer au Québec entre 1996 et 2023.
Les taux ajustés de mortalité sont appropriés. Le cancer touche principalement les personnes d'âge moyen et avancé, et la population du Québec était plus âgée en 2023 qu’en 1996. L’ajustement permet de neutraliser l'effet du vieillissement démographique lors d'une analyse temporelle, en rendant les taux comparables d’une période à l’autre.
- J’aimerais comparer le tabagisme à Montréal et en Gaspésie—Îles-de-la-Madeleine.
L’utilisation de proportions ajustées de fumeurs est nécessaire. En effet, les deux régions peuvent avoir des structures d’âge différentes. Le vieillissement est généralement plus marqué dans les régions rurales telle la Gaspésie, tandis que les régions urbaines comme Montréal tendent à être plus « jeunes » en raison de l'afflux d'étudiants et d'immigrants.
- Je m’intéresse aux données sur les jeunes du secondaire.
Seules les proportions brutes sont présentées pour les indicateurs relatifs aux jeunes du secondaire issus de l’Enquête québécoise sur la santé des jeunes du secondaire (EQSJS). Puisque la gamme d’âge des répondants est restreinte – 12 à 17 ans –, la répartition par âge varie peu d’une région à l’autre ou dans le temps, ce qui rend l’ajustement par âge peu pertinent dans ce contexte.
- J’aimerais analyser l’évolution des troubles anxiodépressifs dans ma région.
Dans ce cas-ci, il peut être utile de combiner les données brutes et ajustées. Les proportions brutes permettent d’estimer le fardeau réel des troubles anxiodépressifs dans ma région, mais il est important de vérifier si la tendance des données brutes concorde avec celle des données ajustées. Si l’ajustement ne modifie pas significativement les tendances, on peut se concentrer uniquement sur les données brutes. En revanche, si les données ajustées révèlent un portrait différent de l’évolution des données brutes, il est important de le mentionner. Ex : « En 2021, 10 % des personnes vivant à Chaudière-Appalaches souffraient de troubles anxiodépressifs, comparativement à 7 % en 2007 (données brutes). Toutefois, lorsque le vieillissement de la population est pris en compte, on constate que la tendance est stable depuis 2007 (selon les données ajustées). »

